Quantum Boundaries in General Quantum Mechanics

Abstract

General Quantum Mechanics (GQM), as proposed by Kiril Chukanov, introduces a framework that challenges conventional physics by incorporating quantum boundaries as fundamental limits shaping the structure and behavior of the universe. These boundaries define zones of ordered matter, influence particle duality, and govern cosmic phenomena such as quasars and free energy processes. This paper explores the key quantum boundaries outlined in Chukanov’s addendum to Volume III of “Universe – That’s Simple!”, including their mathematical formulations, implications for electron-proton duality, and roles in cosmology. By delineating the “Ordered World” and its constraints, quantum boundaries provide a unified explanation for observed discrepancies in mainstream theories, such as dark matter and energy, while proposing mechanisms for quantum free energy generation.

Introduction

General Quantum Mechanics extends traditional quantum theory by introducing world constants and quantum boundaries that dictate the permissible scales and behaviors of matter and energy. Unlike established models reliant on Einstein’s relativity and the Standard Model, GQM posits two intertwined universes: the Electron Matter Universe (space-continuum) and the Proton Matter Universe (visible matter). Quantum boundaries act as thresholds, akin to Planck’s constant but extended to acceleration and spatial limits, enforcing symmetries and preventing violations of universal principles.

Chukanov‘s work critiques “Mathephysics” — the over-reliance on mathematical abstractions without physical grounding — and highlights how quantum boundaries resolve paradoxes in cosmology, particle physics, and energy conservation. This paper synthesizes these concepts, focusing on the boundaries’ definitions, derivations, and applications.

Diagram illustrating quantum boundaries that define ordered matter and cosmic limits in general quantum mechanics

Electron-Proton Duality and Fundamental Constants

At the core of GQM is the electron-proton duality, where the proton is viewed as a “developed” counterpart of the electron. This duality manifests in differing values of fundamental constants between the Electron Matter Universe and Proton Matter Universe.

A key world constant introduced is a0,p, the minimum quantum acceleration in the Proton Matter Universe, analogous to Planck’s constant h:

a_{0, p} \approx \frac{h_{p} \cdot c}{R_{p}^{2}}

where h_p is the Planck constant for proton matter, c is the speed of light, and R_p is the proton radius. This constant underpins the quantum boundaries, ensuring discrete scales in matter formation.

The universes exhibit distinct parameters:

Electron Matter Universe: Constants like h_e, c, e.
Proton Matter Universe: Adjusted values, e.g., h_p, leading to boundaries such as R_h,p.

Visualization of the proton as an evolved electron structure showing matter duality in general quantum mechanics

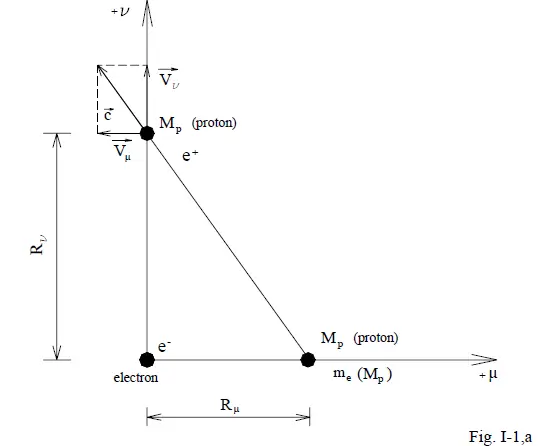
Figure I-1a illustrates this duality, showing the proton as an evolved electron structure with mass M_p and charge separation.

Key Quantum Boundaries

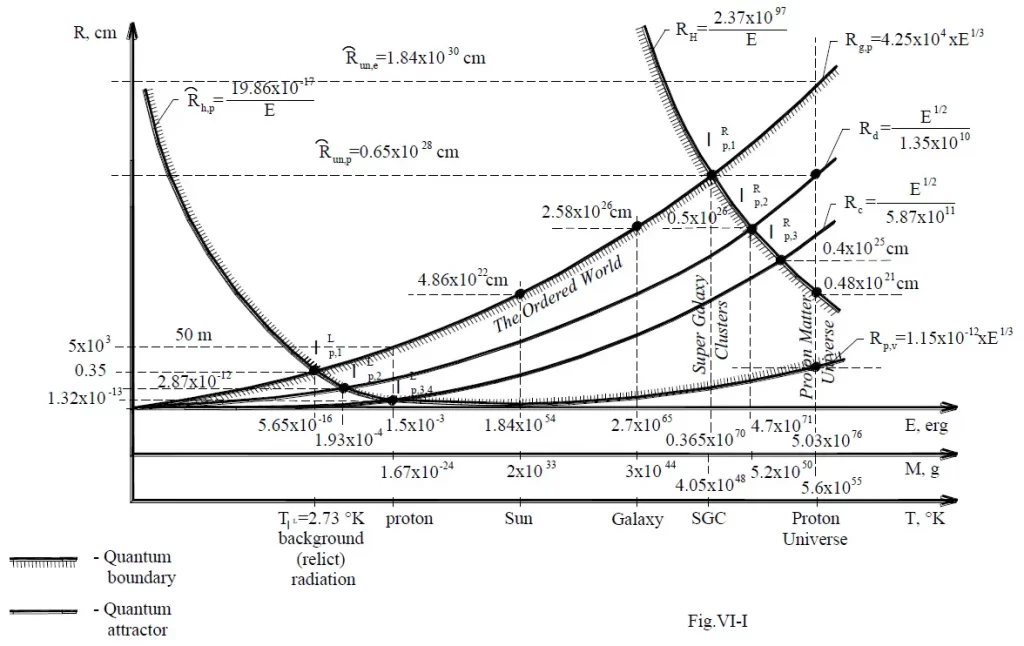
Quantum boundaries define the “Zone of the Ordered World,” where stable matter exists. Below, we detail prominent boundaries from Chukanov’s formulations.

1. Quantum Boundary R_h,p

This is the left-down boundary of the Ordered World in the Proton Matter Universe:

R_{h, p} = \frac{h_{p} \cdot c}{E} = \frac{1.986 \times 10^{- 16}}{E} cm

It represents the minimum spatial scale for given energy E, beyond which matter behaves as a “two-face” continuum. To the left of λ^L_p,1 (a separation point on this boundary), proton matter exhibits dual characteristics, leading to phenomena like background radiation at 2.73 K.

2. Quantum Boundary R_g,p

The upper boundary acting as a repulsive force for baryons:

R_{g, p} = 4.25 \times 10^{4} \cdot E^{1 / 3} cm

For distances ≤ 50 meters between baryons, it induces repulsion. The proton has four “faces” corresponding to boundaries:

Parton: 1.54×10⁻¹⁶ cm
Nucleus: 1.32×10⁻¹³ cm
Nuclear force range: 2.87×10⁻¹² cm
Repulsive baryon: 50 meters

3. Quantum Boundary R_H

A horizon-like boundary for massive objects:

{\bar{R}}_{H} = \frac{2.37 \times 10^{97}}{E} cm

It confines quasars and super-galaxy clusters, with intersection points like x_p,1^R linking multiple boundaries.

4. Quantum Boundary R_λe

Specific to the Electron Matter Universe:

{\bar{λ}}_{e} = \frac{h_{p}}{m_{e} \cdot c} = 3.8614 \times 10^{- 11} cm

This wavelength boundary governs electron behavior in space around proton matter.

Peculiar Points and Symmetries

Separation points like λ_p,4^L divide regimes where different boundaries dominate. For instance, λ_p,2^L corresponds to meson masses (~120 MeV), demonstrating electron-proton symmetry:

M_{λ_{p, 2}^{L}} = 2.15 \times 10^{- 25} g \approx 120 MeV

Cross-points reveal cosmic scales, e.g., universe radius 0.654×10²⁸ cm.

Implications for Cosmology

Quantum boundaries explain phenomena dismissed by mainstream models:

Quasars: Class I quasars exist between r_g and R_H, powered by quantum free energy, not black holes. Class II split into twins due to boundary violations, resolving redshift anomalies without invoking dark energy.
Dark Matter/Energy: Gravitational lensing of quasars results from boundary-induced duplicates, not unseen mass. Dark energy is a mathematical artifact; true expansion balances kinetic (free energy) and negative (gravity, boundaries) energies, maintaining zero total energy.
Universe Structure: Boundaries control mega-formations:
- Super Galaxy Cluster: 2.82×10²⁵ cm
- Galaxy: 0.524×10²¹ cm

Dynamics involve gravity, boundaries, and constants, ensuring equilibrium.

Quantum Free Energy and Boundaries

Boundaries enable free energy in extreme conditions, violating conservation locally to preserve constants. Examples:

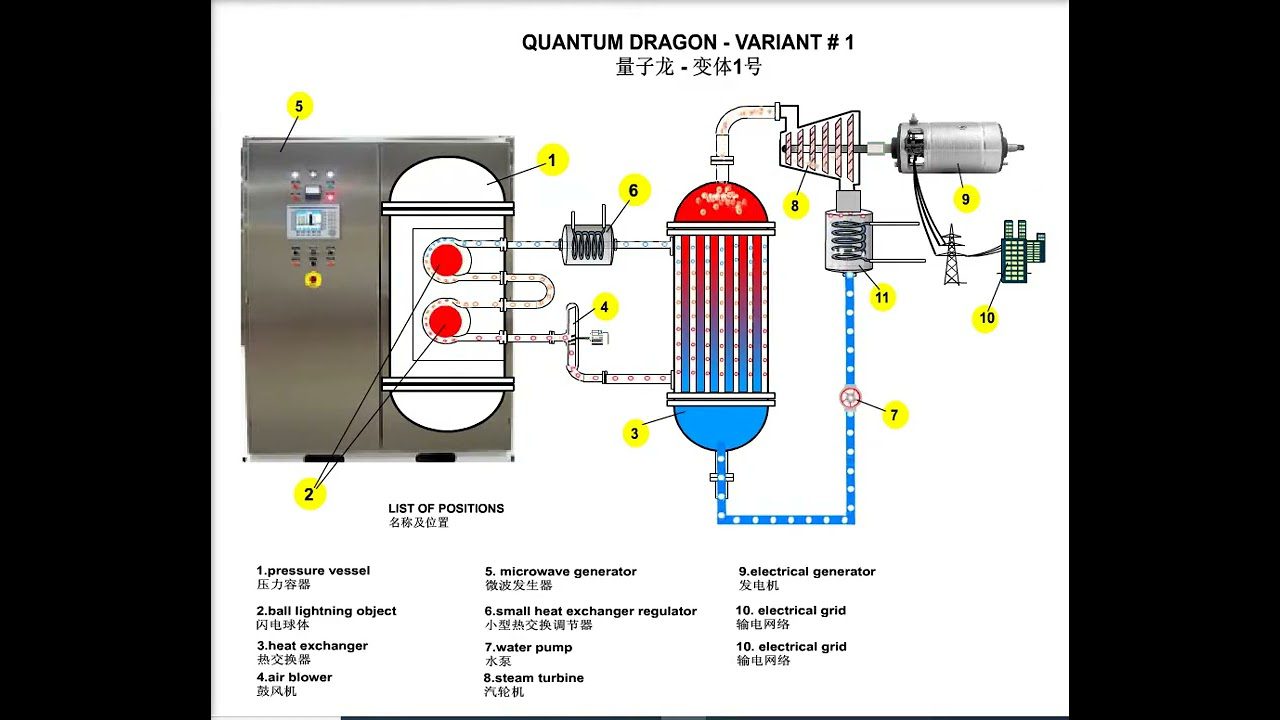
Cosmic ball lightning in stars/quasars generates energy via excitation on R_h,p.
World constants act as sources when laws conflict, e.g., accelerating bodies beyond limits.

In gamma-ray bursts, boundaries amplify explosions in neutron stars.

Conclusion

Quantum boundaries in GQM provide a cohesive framework for understanding the universe’s construction, from particle scales to cosmic structures. By prioritizing physical principles over mathematical constructs, they substantiate claims of free energy and duality, challenging Einsteinian paradigms. Future experiments, such as verifying repulsive baryon forces, could validate these boundaries. As Chukanov asserts, great theories evolve through radical departures, and quantum boundaries may herald such a shift, fostering innovations in energy and cosmology.

References

(Note: Mathematical derivations are reproduced from the source; empirical validation remains a subject for further research.)

Author:

George Stantchev

Bulgarian scientist and innovator with Bachelor, Master and PhD degrees in Physics and Business. Founder and executive director of Chukanov Quantum Energy, Ltd. Author of multiple patents and papers in the field of quantum energy.

D-r George Stantchev

Quantum Boundaries in General Quantum Mechanics

Abstract

Introduction

Electron-Proton Duality and Fundamental Constants